MESURE - Mesures optiques

MESURE - Mesures optiques

Par mesures optiques, il faut entendre les mesures faites grâce à la lumière. En ce qui concerne les mesures faites sur la lumière, le lecteur se reportera aux rubriques PHOTOMÉTRIE, pour les mesures d’énergie, SPECTROSCOPIE, pour les mesures de fréquence et de longueurs d’onde, et LUMIÈRE – Polarisation, pour les mesures ellipsométriques.

La dix-septième Conférence générale des poids et mesures, réunie à Paris en octobre 1983, donne un rôle important à la lumière en définissant le mètre comme l’une des principales unités de base du Système international d’unités: «Le mètre est la longueur du trajet parcouru par la lumière dans le vide en une durée de 1/299 792 458 de seconde.»

Que ce soit par la mesure du temps de vol d’une impulsion brève ou par interférométrie, le laser, qui est à l’origine de cette définition, joue un rôle essentiel non seulement en ce qui concerne les étalons et la métrologie fondamentale, mais également dans les applications telles que les instruments de mesure des longueurs et des distances ainsi que dans les mesures et les contrôles industriels. Depuis longtemps, la propagation rectiligne de la lumière est mise à profit dans des instruments tels que l’alidade. Aujourd’hui, l’emploi d’une lunette et de détecteurs photoélectriques permet d’atteindre les limites ultimes permises par la structure ondulatoire de la lumière: les lunettes autocollimatrices pour les mesures d’angles, les microscopes photoélectriques pour les mesures de positions et de déplacements. La propagation rectiligne est exploitée dans les mesures géométriques à deux et trois dimensions: contrôle des surfaces optiques, des ouvrages d’art et des monuments historiques, cartographie par photographie aérienne ou spatiale, métrologie tridimensionnelle.

Le plus léger de tous les palpeurs, le rayon de lumière, est le moins perturbateur. Sa grande vitesse de propagation en fait un outil remarquable de contrôle rapide et en temps réel sur des objets en mouvement.

1. Mesures de longueurs, de distances et de déplacements

Mesures de temps de propagation

Une mise en pratique de la définition du mètre est la détermination de la distance de la Terre à la Lune par la mesure du temps de vol aller et retour d’une impulsion lumineuse brève. Cette technique fut mise en œuvre bien avant la définition de 1983, en particulier en France à l’observatoire du Centre d’études et de recherche géodynamiques et astronomiques (C.E.R.G.A.) situé au-dessus de Grasse. On exploita tout d’abord les propriétés d’un laser à rubis. Une impulsion de 1 J, dont la durée est de 1 ns (puissance instantanée 1 GW), est focalisée par un miroir de 1,5 m de diamètre puis est réfléchie par les panneaux de cataphotes («coins de cube») déposés en plusieurs lieux sur la Lune (fig. 1). Le même télescope collecte les quelques photons rescapés de l’aventure; de l’ordre de 10¹⁹ au départ, ils ne sont plus que quelques-uns au retour. Le temps de vol aller et retour de l’impulsion, qui est de l’ordre de 2,5 s, est ainsi déterminé avec une incertitude de quelques dixièmes de nanoseconde. L’incertitude sur la distance parcourue, après correction de la traversée de l’atmosphère qui ralentit les ondes électromagnétiques, est de 10 à 15 cm. Grâce à la très grande distance parcourue, cette mesure permet d’approcher au mieux l’exactitude dans la mesure des longueurs par l’étalon-lumière. Des satellites artificiels (Starlette, Diadème) truffés de cataphotes analogues permettent de déterminer les distances entre stations terrestres avec une incertitude du même ordre de grandeur et de connaître la morphologie de notre Planète avec une acuité inconnue jusqu’ici.

Mesures de déphasage

La limite de résolution temporelle des détecteurs les plus rapides interdit d’appliquer la méthode précédente à des distances trop courtes. En effet, si l’on sait générer avec certains lasers des impulsions dont la durée est inférieure à 1 ps, aucun détecteur ne permet de fixer une impulsion, même énergique, à moins de quelques dizaines de picosecondes. En 10 ps, la lumière parcourt 3 mm et les détecteurs d’un coût raisonnable ne permettraient pas de descendre au-dessous d’une trentaine de millimètres. Cette difficulté est évitée en remplaçant la détection d’une impulsion par la mesure du déphasage d’une onde modulée en haute fréquence. Un détecteur dont la constante de temps est de 1 ns et la bande passante de 1 GHz. Avec ce détecteur, on peut mesurer sans grande difficulté des variations de phase avec une incertitude de 10^-3 rad. Sur une onde modulée à une fréquence de 100 MHz, l’incertitude est celle que donnerait un détecteur de 2 ps de constante de temps. La résolution spatiale correspondante est de 0,3 mm, résolution intéressante pour la mesure de distances allant de quelques mètres en environnement difficile (contrôle des parois d’un four) à quelques kilomètres. Pour ce dernier cas, la principale cause d’incertitude provient de l’indice de l’air traversé n = c /c , où c est la vitesse de la lumière dans le vide connue exactement, et c la vitesse dans l’air. L’indice varie également avec la température et la pression (entre autres paramètres).

Mesures interférométriques

Pour les distances plus courtes, de quelques micromètres à quelques mètres, c’est l’interférométrie qui permet d’aller beaucoup plus loin dans la résolution spatiale. Les fréquences optiques sont de l’ordre de 500 THz (5 憐 10¹⁴ Hz) et l’interféromètre de Michelson permet de visualiser la longueur d’onde sous forme d’un signal photoélectrique sinusoïdal. En laboratoire, il n’est pas très difficile de mesurer l’angle de phase à 10^-3 frange près. Cette mesure est équivalente à ce que donnerait la détection d’une impulsion avec une résolution temporelle de 2 憐 10^-19 s, soit une résolution spatiale égale à 0,03 nm (3 憐 10^-11 m). Cette distance est plus faible que celle qui sépare deux couches atomiques dans un cristal.

Avec une résolution plus modeste de l’ordre du dixième de frange, l’interféromètre à laser permet de mesurer les déplacements rectilignes sur les machines à mesurer ou les machines-outils avec une incertitude pouvant descendre, dans les conditions les plus favorables, à quelques centièmes de micromètre. Cette mesure permet un transfert très direct de la définition de l’unité de longueur depuis le laboratoire de métrologie jusque dans les ateliers de mesure industrielle: la fréquence du laser est étalonnée au laboratoire avec une précision qui ne dépend que du laser lui-même par comparaison avec un laser de référence qui est stabilisé par absorption saturée dans la vapeur d’iode ( 益 = 473 612 214 836 kHz à 1,6 dix-milliardième près). La longueur d’onde du laser est calculée en temps réel dans l’atelier de mesure grâce à cette fréquence avec une correction sur la valeur de l’indice de l’air.

Pour étalonner les règles jusqu’à 3 m de longueur, le Laboratoire national d’essais dispose d’un banc interférométrique équipé d’un microscope électronique. Le microscope se déplace au-dessus de la règle sur des patins à coussin d’air et détecte le passage des traits fins gravés sur la surface polie (largeur des traits entre 5 et 20 猪m). Trois interféromètres, éclairés par le même laser stabilisé, déterminent l’amplitude des translations de trois réflecteurs en «coin de cube» solidaires du support du microscope. On peut ainsi détecter les défauts de translation du microscope (lacet et tangage) et en corriger l’effet sur la position du point de visée du microscope. La distance entre les traits gravés sur une règle de référence peut ainsi être déterminée avec une incertitude de quelques dixièmes de micromètre sur 3 m.

L’interférométrie peut aussi être employée de manière tout à fait différente pour la détermination de l’épaisseur des cales de référence utilisées dans les ateliers de métrologie dimensionnelle. On observe à l’aide d’un interféromètre de Michelson, éclairé par une radiation monochromatique de longueur d’onde dans l’air¹, les franges de coin d’air formées entre un miroir plan et la cale d’épaisseur e adhérée sur un plan de référence. Le décalage mesuré entre les deux systèmes de franges donne accès à l’excédent fractionnaire 﨎¹ sur la variation de différence de marche:

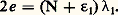Comme les franges ne sont pas numérotées, il n’est pas possible d’avoir accès par cette simple expérience au nombre entier N qui sépare les ordres d’interférence observés sur la cale et sur le plan de référence. Pour atteindre N, on effectue la même mesure d’excédent fractionnaire avec une autre radiation de longueur d’onde². Comme on connaît déjà l’épaisseur e de la cale à quelques micromètres près, on trouve ainsi sans ambiguïté la seule valeur de e qui donne les deux valeurs 﨎¹ et 﨎². Par précaution, et à titre de vérification, on effectue en général cette mesure avec quatre radiations de longueur d’onde connue. À l’Établissement technique central de l’armement à Arcueil, un interféromètre de Michelson, qui mesure ainsi les cales jusqu’à 100 mm d’épaisseur, est couplé à une caméra électronique et un ordinateur. L’image des franges est numérisée, traitée en temps légèrement différé et on obtient une carte des variations d’épaisseur de la cale avec une résolution voisine de 10 nm (fig. 2).

Règles et codeurs optiques

Les règles optiques sont moins sensibles à l’environnement que les interféromètres et sont très appréciées pour l’automatisation des mesures et la commande des machines, avec une résolution de l’ordre de 1 猪m. Un réseau, dont le pas est en général égal à 20 猪m, se déplace le long d’une règle sur laquelle est gravée une échelle au même pas. Les franges de moiré qui défilent sont comptées et une interpolation sur le signal de franges permet d’atteindre une résolution de 1 猪m. Comme pour l’interférométrie, la mesure est incrémentale et un système de deux réseaux en quadrature de phase permet de lever l’ambiguïté sur le sens du déplacement et de réaliser un comptage réversible. Ces systèmes ont une grande qualité métrologique, car l’intégration avec les franges de moiré et la moyenne sur un grand nombre de traits du réseau éliminent l’influence des défauts locaux de la gravure.

Règles codées et incrémentales peuvent être gravées sur une circonférence et donner des mesureurs et des codeurs angulaires (fig. 3), dont les modèles les plus compacts trouvent de nombreux débouchés dans la réalisation des robots. Sur un disque de 50 mm de diamètre, une gravure de 18 000 traits et une interpolation au centième de pas permettent de mesurer les rotations avec une incertitude inférieure à une seconde d’arc (il y a 1 296 000 s/tr).

2. Mesures de vitesses

Vélocimétrie Doppler par laser

Dans les techniques interférométriques précédemment décrites, la mesure est celle d’un déplacement et s’effectue par un comptage des franges. La fréquence f = 2v/ du signal interférentiel monochromatique issue d’un interféromètre, dont le réflecteur mobile se déplace à la vitesse v, peut être interprétée comme le signal de battement entre la radiation réfléchie par le miroir fixe et celle que réfléchit le miroir mobile, et dont la fréquence est décalée par effet Doppler-Fizeau. Compter les franges revient à intégrer cette fréquence proportionnelle à la vitesse et permet de déterminer la position du réflecteur mobile par la relation:

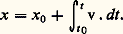Cela est appliqué pour une méthode de mesure de la vitesse, où l’on détecte la fréquence de battement entre la lumière parfaitement monochromatique, émise par un laser continu, et cette lumière diffusée par des particules en mouvement. L’anémométrie laser est utilisée en débitmétrie, dans l’analyse des turbulences, avec des dispositifs permettant d’atteindre les trois composantes des vecteurs vitesse, et en analyse biomédicale (mesures sur la circulation sanguine, la mobilité des spermatozoïdes).

Une autre méthode moins délicate peut être exploitée, qui consiste à faire interférer dans une petite région de l’espace deux ondes planes monochromatiques, issues d’un même laser de longueur d’onde et générer ainsi un réseau de franges planes, parallèles et équidistantes de pas p =/ , où est l’angle que forment les deux faisceaux. Une particule qui traversera ce réseau de franges avec une composante de vitesse v dans la direction perpendiculaire au plan des franges diffusera de la lumière modulée à la fréquence f = v /.

Une analyse fréquentielle des modulations de la lumière diffusée donnera un histogramme de cette composante des vecteurs vitesse des particules diffusantes.

La mesure des rotations

L’interférométrie est aussi un outil de choix pour la mesure absolue des rotations sans référentiel matériel. Avec les translations, c’est une mesure de ce genre qu’espéraient faire Albert Michelson et Edward Morley en 1887 pour détecter la translation absolue de la Terre par rapport à l’espace. Cette tentative fut un échec, mais conduisit à l’élaboration par Albert Einstein de la théorie de la relativité. A. Sagnac montra par contre en 1913 que l’expérience pour détecter une rotation pouvait être faite avec un interféromètre en anneau, l’effet attendu étant alors du premier ordre et s’interprétant parfaitement dans le cadre de la théorie classique de l’effet Doppler-Fizeau. Lorsqu’un tel interféromètre est éclairé par une radiation monochromatique de longueur d’onde, et qu’il est immobile, la différence de marche est nulle, aux défauts de symétrie près, les deux faisceaux parcourant le même trajet en sens inverses. Si l’interféromètre tourne autour d’un axe perpendiculaire au plan de la figure 4, le faisceau qui se propage dans le sens de la rotation parcourt un trajet allongé et l’autre faisceau un trajet raccourci. Mis en rotation avec une vitesse angulaire constante 諸 autour de cet axe, l’interféromètre présente une différence de marche L proportionnelle à 諸 et à la surface S délimitée par le trajet des faisceaux lumineux: L = 諸 憐 4 憐 S/c .

Les fibres optiques ont apporté à cet interféromètre un regain d’intérêt en multipliant la surface par l’accumulation de plusieurs milliers de spires. Les gyromètres à fibre optique remplacent parfois les gyroscopes mécaniques dans les plates-formes de navigation. Ils présentent l’avantage considérable de n’avoir aucune pièce mobile, et leur sensibilité est telle qu’ils peuvent détecter une vitesse de rotation égale au millième de la vitesse de rotation terrestre. Des gyromètres à fibre optique de faible coût pourraient bientôt figurer dans la panoplie des équipements de l’automobile. Le gyrolaser, qui mesure par battement le décalage de fréquences de deux modes se propageant en sens contraires dans un laser en anneau, est une alternative à ce capteur de rotation. Une centrale inertielle à trois gyrolasers équipe le lanceur européen Ariane IV.

3. Les pointés angulaires

La propagation rectiligne

La lumière se propage en ligne droite dans le vide ou dans un milieu homogène. Cette propriété fondamentale est à la base de l’un des premiers instruments de mesure: l’alidade avec laquelle les astronomes et les navigateurs firent les premières mesures de qualité. Les alidades modernes améliorent les possibilités de l’œil par l’utilisation d’une lunette afocale et d’un réticule. Les pointés deviennent impersonnels grâce aux détecteurs photoélectriques. On peut ainsi mesurer de petits angles dans un champ de l’ordre de quelques degrés où les distorsions de l’objectif peuvent être négligées (fig. 5).

La sensibilité de détection d’une petite variation de direction (limite de résolution angulaire) est imposée par le phénomène de diffraction. La largeur angulaire de la tache de diffraction d’une pupille circulaire sans aberration de diamètre D est exprimée en radians: 﨎 = 1,22/D, soit environ 3 pour D = 50 mm. Grâce aux lunettes photoélectriques, on peut repérer une direction avec une sensibilité cent fois meilleure, et faire des pointés sur un même miroir avec des défauts de reproductibilité de quelques centièmes de seconde d’arc. La lunette autocollimatrice qui émet un faisceau collimaté et reçoit ce faisceau après réflexion sur un miroir plan de bonne qualité est un remarquable instrument de pointage d’une direction de référence (fig. 6). Utilisée comme pointeur de zéro avec un prisme à 5, 7 ou 11 faces, cet instrument permet l’étalonnage des plateaux diviseurs avec une exactitude qui ne dépend que des dimensions des faces des prismes et de leur planéité.

Photogrammétrie

Avec un objectif spécialement calculé pour l’élimination des distorsions (objectif à grand champ mais de faible ouverture numérique), on peut enregistrer une image sur laquelle des mesures de distances se traduiront en mesures angulaires. En comparant deux clichés pris sous deux angles différents, il est possible de restituer, par un traitement de données ultérieur très élaboré, la disposition des points de l’objet dans l’espace tridimensionnel. D’abord appliquée avec succès par l’Institut géographique national à la cartographie par photographie aérienne, la photogrammétrie a été utilisée pour la sauvegarde des temples de la haute vallée du Nil menacés par la construction du barrage d’Assouan. Elle est exploitée maintenant pour transformer notre patrimoine architectural en fichiers de données numériques que des machines spécialisées peuvent restituer en vues saisissantes, métrologiquement fidèles à l’original. C’est par ce procédé que les ateliers de moulage du musée du Louvre peuvent proposer de splendides répliques des objets les plus divers allant de la Frise des prisonniers asiatiques extraite d’un temple de Nubie à la Vénus de Milo ou la Victoire de Samothrace ^{[cf. PHOTOGRAMMÉTRIE]}.

Les prismes réflecteurs

La propagation rectiligne et les lois de la réflexion sont également exploitées dans des dispositifs optiques simples mais de grande qualité: les équerres optiques et les trièdres trirectangles ou «coins de cube». L’équerre optique est l’ensemble de deux miroirs plans formant un dièdre égal à 45⁰. Tout rayon incident dans un plan de section principale (plan perpendiculaire à l’arête du dièdre) repart perpendiculairement au rayon incident, indépendamment de l’angle d’incidence. Tout rayon incident sur un coin de cube repart parallèlement à lui-même après réflexion sur les trois faces du trièdre, quelle que soit sa direction d’incidence. Cette propriété remarquable est mise à profit dans les rétroréflecteurs utilisés comme cibles dans les mesures géodésiques (mesures de distances par laser, réflecteurs lunaires, satellites géodésiques) ou comme réflecteur mobile en interférométrie.

La turbulence atmosphérique

Dans les pointés angulaires, la diffraction n’est une limite qu’en laboratoire et pour des visées à courte distance (quelques mètres au plus). Dès que la portée des instruments augmente, les hétérogénéités et les instabilités de l’air traversé sont une limitation bien plus sévère: elles limitent cette précision à quelques secondes d’arc ou quelques dizaines de secondes suivant les conditions. Le contrôle d’un bon miroir de télescope est limité par cette turbulence; de plus, les stratifications de l’indice en atmosphère calme déforment les trajectoires des rayons, c’est pourquoi, pour que les qualités de l’image donnée dans l’espace par le télescope spatial de 2 m de diamètre ne soient limitées que par la diffraction, le contrôle de sa forme doit s’effectuer dans le vide.

L’astrométrie, science des mesures angulaires par excellence, est limitée dans les mesures au sol par la turbulence de l’atmosphère. Cette barrière de la résolution angulaire a été franchie de manière spectaculaire par A. Labeyrie à l’aide de deux techniques mises en œuvre dans les observatoires français et aux États-Unis. En prenant une photographie avec un temps de pose court, devant la constante de temps de la turbulence, l’astronome enregistre une structure complexe, dite de speckle. Un traitement de signal numérique a posteriori permet de retrouver des informations sur la structure spatiale de l’objet avec la limite de résolution théorique du télescope.

Par ailleurs, reprenant une méthode suggérée par Hippolyte Fizeau dès 1860 et mise en œuvre par A. Michelson, A. Labeyrie a étudié de la même manière les franges d’interférence données au voisinage de la différence de marche nulle par deux télescopes pointés sur la même étoile. La distance entre les télescopes peut être changée, réalisant ainsi une véritable synthèse d’ouverture dans le domaine optique comparable à ce qui est fait maintenant couramment en radioastronomie. À l’aide de deux télescopes de 25 cm de diamètre, les collaborateurs de A. Labeyrie ont pu mesurer à l’observatoire du C.E.R.G.A. des structures stellaires avec une résolution angulaire meilleure que le millième de seconde d’arc, reconstituant pour la première fois par une série de mesures faites à des époques différentes la trajectoire elliptique de Capella dans la constellation du Cocher, autour de son compagnon stellaire indiscernable sur nos plus grands télescopes.

4. Contrôle des formes

Mesures de planéité et de rayons de courbure

L’interférométrie permet de comparer deux formes simples comme des plans et des calottes sphériques. Dans la mesure des épaisseurs de cales, l’analyse de la forme des franges données entre la face supérieure de la cale et le miroir plan de l’interféromètre donne les défauts de forme de cette face avec une sensibilité du centième de frange (3 nm). L’interféromètre de Twyman-Green (fig. 7) est une forme de l’interféromètre de Michelson qui permet de tester la planéité d’une surface d’onde. L’association d’un objectif et d’un miroir sphérique supposé parfait permet de tester le stigmatisme de cet objectif, en observant les écarts de l’onde réfléchie après double passage dans l’objectif et réflexion sur le miroir sphérique, par rapport à l’onde plane donnée par l’autre bras de l’interféromètre. Les principales aberrations se révèlent sous forme de franges de forme caractéristique et peuvent être numériquement évaluées.

Pour les plans et les surfaces sphériques, les franges données par les lames minces conduisent au même résultat avec un minimum de moyens (fig. 8). En accolant la surface E à tester contre un calibre R, on observe les franges de coin d’air formées dans la lame mince d’air qui les sépare, et la forme de ces franges trahit avec une grande sensibilité les écarts de forme entre les deux surfaces. Le centième de frange peut être atteint, ce qui correspond à 1/200 de longueur d’onde dans le défaut géométrique, pourvu que l’on prenne certaines précautions dans l’éclairage de la lame mince pour que les franges y soient bien localisées. La méthode est différentielle et suppose une référence parfaite. Mais l’observation des franges données par trois combinaisons deux à deux de trois plans permet de dresser une carte des défauts de planéité absolus de chacun des trois plans.

Ces contrôles interférométriques sont efficaces pour des surfaces très simples: plans, calottes sphériques de grand rayon de courbure par rapport au diamètre. On peut également contrôler des surfaces plus complexes (surfaces asphériques) en synthétisant la surface d’onde de référence à l’aide d’un hologramme calculé. La grande exactitude de tracé de cet hologramme garantit la qualité de la surface d’onde ainsi synthétisée.

Les techniques interférométriques précédentes ne s’appliquent qu’à des surfaces polies optiquement. L’holographie permet d’aller plus loin et de visualiser des franges entre deux images d’un objet de forme et d’état de surface quelconques. Grâce à l’enregistrement photographique, l’holographie permet de faire interférer un objet avec lui-même en deux instants différents, ou d’observer en temps réel les interférences d’un objet avec son image holographique prise comme référence. L’interférométrie holographique a ainsi ouvert la voie à de nombreux contrôles industriels non destructifs. C’est un moyen d’étude efficace des défauts de structures: fissures, collages, hétérogénéité des matériaux. Il faut noter que, si la prise d’un hologramme sur un long temps de pose nécessite un environnement exceptionnellement stable, la prise d’hologrammes avec des lasers à impulsions peut se faire dans les environnements les plus instables et avec des objets animés de vitesses importantes. Une impulsion de 1 ns permet l’observation de franges contrastées avec des vitesses radiales allant jusqu’à 250 m/s. Un hologramme en double exposition pris avec deux impulsions brèves rapprochées permet d’établir une carte bidimensionnelle des vecteurs vitesse dans un processus à évolution très rapide, voire explosif.

Contrôles de rectitude et de planéité

Les mesures de rectitude ne sont pas aussi simples que pourrait le laisser croire le principe de la propagation rectiligne. En effet, il existe une relation d’incertitude dans le domaine spatial, imposée par la propagation des ondes de toute nature, entre la directivité d’un faisceau de rayons et sa localisation. C’est le phénomène de diffraction, qui est à l’origine de cette limitation et que l’on peut traduire par une constance du produit d . , d étant le diamètre du faisceau et son angle de divergence: d . 年.

Si l’on veut contrôler une rectitude sur une longueur L, le diamètre d du faisceau doit être suffisant pour que l’angle de divergence =/d n’excède pas d /L. On en déduit que le diamètre du faisceau d doit être au moins égal àL. Pour L = 1 m, cela donne d = 0,7 mm. Pour contrôler une rectitude à 梁 1 猪m près, il faut donc pouvoir repérer le centre du faisceau avec une incertitude égale au millième de sa largeur. On obtient ce résultat avec une cellule à quatre quadrants dont les signaux convenablement filtrés sont comparés deux à deux par un dispositif électronique. Par contre, avec un faisceau de 1 cm de diamètre, il est trivial de contrôler une rectitude au millimètre près sur plusieurs centaines de mètres. Les alignements par lasers sont maintenant d’usage courant sur les chantiers de travaux publics et les ouvrages d’art, dans le percement des tunnels ou la construction des barrages.

La lunette autocollimatrice est également un outil très utile pour contrôler la rectitude d’une glissière. Un miroir plan monté sur un support prenant appui en deux points A et B sur la trajectoire à contrôler a une orientation déterminée par la moyenne de la pente dh /dx entre ces deux points. La lunette autocollimatrice permet d’enregistrer point par point cette orientation et d’en déduire par intégration le profil de la glissière. L’interféromètre à laser muni d’un accessoire destiné à la mesure des petites rotations permet la même opération (fig. 9). À partir de la combinaison d’une série bien choisie de mesures de rectitude, on peut par ces méthodes tracer la carte des défauts de planéité d’un marbre.

La propagation rectiligne de la lumière permet également de contrôler très simplement la forme sphérique d’une surface d’onde. C’est la méthode de Foucault, destinée à caractériser l’image I d’une source ponctuelle O et schématisée sur la figure 10. L’œil ou un récepteur d’image étant placé derrière le point de focalisation I des ondes sphériques, on place au voisinage de ce point un couteau fin C à l’aide duquel on coupe les rayons. Si le couteau est placé avant le point I en C¹, on voit le champ de lumière s’obscurcir par une ombre qui se déplace dans le même sens que le couteau. En position médiane, le couteau donne un champ dont l’aspect est donné en P². Si ce couteau est placé après le point de focalisation en C³, l’ombre se déplace dans le sens contraire et le champ se présente comme en P³. Si le couteau est correctement placé au point F et si la surface d’onde est bien sphérique, le champ s’obscurcit uniformément, les plages S¹ et S² restent identiques. L’œil qui, couplé au cerveau, est un analyseur d’image remarquable détecte par cette méthode des hétérogénéités d’éclairement du champ qui mettent en évidence des défauts de forme des surfaces d’onde dont l’amplitude est de l’ordre du dixième de la longueur d’onde. V. Ronchi a décrit un test dont l’interprétation est plus délicate mais qui utilise un réseau de moiré et son image au lieu d’une source ponctuelle et d’un couteau, ce qui la rend beaucoup plus lumineuse et facile à mettre en œuvre.

Fonction de transfert de modulation

Les dispositifs de ce contrôle de la forme d’une onde lumineuse se caractérisent par leur réponse impulsionnelle, qui correspond à la répartition de l’énergie lumineuse donnée dans l’image d’un objet ponctuel. Plutôt que d’analyser cette répartition d’éclairement dans une image quasi ponctuelle, on préfère examiner l’image d’un objet périodique (un réseau de pas p , donc de fréquence spatiale 1/p ) et mesurer en amplitude et en phase la répartition d’éclairement. Le rapport des amplitudes des variations d’éclairement dans l’objet et dans l’image, appelé fonction de transfert de l’imageur, est un nombre complexe dont le module tend vers zéro quand la période de l’objet s’approche de la limite de résolution spatiale de l’objectif. Cette fonction de transfert permet de revenir par transformation de Fourier dans l’espace à deux dimensions à la réponse impulsionnelle (cf. OPTIQUE – Images optiques). Il est plus commode de déterminer expérimentalement la fonction de transfert de modulation d’un objectif que sa réponse impulsionnelle. Les utilisateurs de microscope pratiquaient la méthode bien avant qu’elle soit généralisée par l’emploi des calculateurs numériques en observant des objets naturels aux fréquences spatiales bien caractérisées comme les diatomées (cf. LUMIÈRE – Diffraction de la lumière).

5. Mesures des indices

Ce sont des pointés goniométriques, effectués sur des prismes, qui permettent, par application des lois de Descartes, la détermination des indices de réfraction, c’est-à-dire du rapport n = c /c : c la vitesse de la lumière dans le vide et c la vitesse dans le matériau. La précision de la détermination de n ne dépend en général que de la qualité du prisme que l’on peut fabriquer avec le matériau, qualité de ses faces (planéité, état de surface) et homogénéité du matériau.

L’indice de réfraction des gaz est trop peu différent de l’unité pour être atteint par ces mesures. La réfractométrie interférentielle est alors un moyen bien adapté, car elle mesure directement n 漣 1 en évaluant la variation de la différence de marche (n 漣 1)l dans un interféromètre dont un des bras de longueur l est mis sous vide puis rempli du gaz dont on veut déterminer l’indice (fig. 11). Une cuve de 20 cm de longueur permet de déterminer l’indice de l’air à la pression atmosphérique avec une incertitude de l’ordre de 10^-8 en mesurant une variation de différence de marche de 250 franges avec une précision de un centième de frange.

L’interférométrie est également bien adaptée pour étudier les gradients d’indice dans une veine gazeuse (étude des écoulements en soufflerie subsonique, transsonique ou supersonique). On utilise l’interféromètre de Mach-Zehnder (fig. 12), qui permet de localiser les franges de coin d’air loin des miroirs ^{[cf. INTERFÉRENCES LUMINEUSES]} ainsi que l’interférométrie holographique.

L’indice de l’air

La modélisation faite en 1966 par B. Edlen à partir d’un grand nombre de déterminations expérimentales donne l’indice de l’air avec une incertitude de l’ordre de 10^-8 pour toutes les longueurs d’onde du spectre visible:

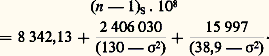où (n 漣 1)^S est l’écart à l’unité de l’indice de l’air sec dans les conditions de référence (15 ⁰C, 101 325 Pa) et 靖 le nombre d’ondes exprimé en 猪m^-1. Les variations de n 漣 1 avec la température T mesurée en kelvins et la pression P mesurée en pascals s’expriment simplement en première approximation en supposant que l’air est un gaz parfait:

B. Edlen a également proposé une expression corrigée pour des conditions éloignées des conditions de référence, en présence de vapeur d’eau et de gaz carbonique.

Dans ces mesures, c’est de la vitesse de phase qu’il s’agit. Quand on mesure une distance dans l’air par temps de vol d’une impulsion ou par déphasage d’une modulation, c’est de l’indice de groupe n ^g qu’il faut se servir: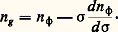

Sur de grandes distances, il est difficile d’avoir une bonne connaissance sur les répartitions de température et de pression. Une méthode consiste alors à mesurer les temps de vol ou les déphasages pour deux radiations de longueurs d’onde différentes. La formule d’Edlen permet une parfaite connaissance de la dispersion de l’air qui est proportionnelle à n 漣 1, donc à la correction qu’il faut apporter à la vitesse moyenne des ondes sur leur trajectoire. C’est le principe de mesure des distances à deux longueurs d’onde qui se révèle à l’heure actuelle comme le meilleur moyen de déterminer la vitesse effective des ondes électromagnétiques en milieu atmosphérique.

Encyclopédie Universelle. 2012.